われわれが慣れ親しんできた従来型のコンピューター（以下「古典的コンピューター」）は、ガリレオ・ガリレイやアイザック・ニュートンらの偉大な物理学者が16～18世紀に切り拓いた古典力学を基に設計されている。

　具体的には、あらゆるデータを0と1から成る二進法で表現。電気が流れている状態（＝オン）を1、流れていない状態（＝オフ）を0として計算を実行する。古典的コンピューターの開発は、この電気的なスイッチを「小さく」あるいは「増やす」ことを目指して進められてきた。

　これに対し、量子コンピューターは20世紀に確立した量子力学の理論を応用する。量子の代表格は原子や電子、光子などだが、いずれも極めて微小であり、ナノ（＝10億分の1）メートルのレベルだ。これを計算用のスイッチに使うと、古典的コンピューターのそれよりずっと小さくできる。

　しかも、量子は後述する「重ね合わせ」と呼ばれる性質を応用することにより、「0であると同時に1でもある」状態を実現できる。コインの表を「0」、裏を「1」で表すと、回転中のコインが0か1か確定していない状態になる。これを量子コンピューターのスイッチに応用すれば、「0か1」しか扱えないスイッチを持つ古典的コンピューターに比べ、はるかに複雑な計算ができるようになる。

量子のスイッチ「０であると同時に1でもある」状態
（出所）リコー経済社会研究所

　この量子コンピューターの仕組みを理解するには、まず量子力学の基本概念を知る必要がある。ここでは、特に重要な①量子②重ね合わせ③もつれ―について説明する。

量子の世界

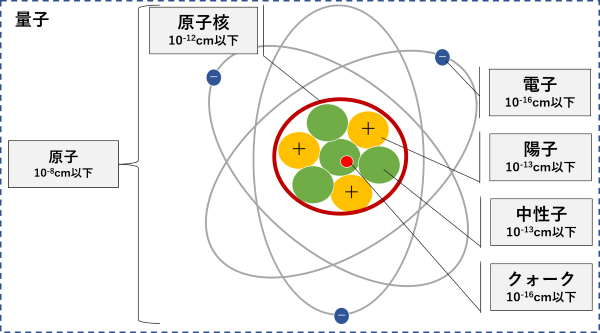
　「量子」とは、大きさが原子以下の「粒」を指す。そもそも原子を意味するアトムの語源は、古代ギリシャ語で「これ以上分割できないもの」という意味。つまり、かつては「原子より小さなものは存在しない」と考えられていたのだ。

　その原子の直径は1000万分の1センチ以下。髪の毛の太さが100分の1センチだから、その10万分の1以下になる。その原子の構成要素である電子は、1000兆分の1センチとケタ外れに小さい。

量子の世界
（出所）リコー経済社会研究所

　ただし、量子は単なる「粒」ではない。実は「波」としての性質を併せ持つのである。例えば、量子の一種である光はプリズムに通すと、屈折して7色に分かれる。この現象が起こるのは、それぞれの色の波長の違いによって屈折率が異なるためであり、光が波であることの証拠になる。

　一方で、光は「光子」という「粒」の集まりでもあり、1粒ずつ飛ばすことも可能。同じ光でも、状況によって「波」の性質を示したり、「粒」の性質を示したりするのである。

　このように「粒であると同時に波でもある」という量子の性質は、従来の古典力学の理論に反していたため、かつては多くの異論が唱えられた。しかし今では、さまざまな実験結果によって矛盾なく説明できるようになり、この量子の性質が定説となっている。

重ね合わせ＝「0であると同時に1でもある」状態

　「重ね合わせ」とは、同じ量子の中に2つ以上の相反する状態が共存する現象。先に述べた「0であると同時に1でもある」状態はその1例になる。

　オーストリアの物理学者エルヴィン・シュレーディンガーは、この状態を説明するため、「シュレーディンガーの猫」と呼ばれる有名な例え話を作った。単純化すると以下のようになる。

シュレーディンガーの猫
（出所）リコー経済社会研究所

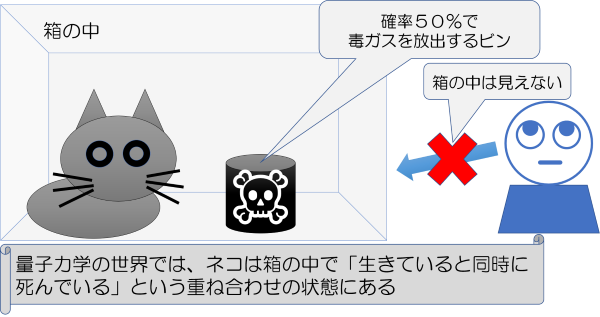
　外からは中の様子が分からない箱を用意し、ネコを閉じ込める。箱の中には毒ガスを詰めたビンも一緒に入っており、確率50%で毒ガスを放出する。箱を開けたとき、ビンが壊れていなければネコは生きている。逆に、ビンが壊れていればネコは死んでいる。

　このとき、われわれが目にしている世界では、箱の中のネコの状態は「生きている」か「死んでいるか」の2種類しかない。つまり中の様子が分からなくても、実際にはネコの生死は箱を開ける前に「決まっている」のである。

　これに対して量子力学が支配する世界では、箱の中のネコは「生きていると同時に死んでいる」という重ね合わせの状態にある。そして、箱を開けて中を「観察」した瞬間、生か死か、どちらか一方に確定する。繰り返しになるが、箱を開けるまで「生死が分からない」のではなく、箱を開けるまでは「生死が重なった状態にある」と考えてほしい。

　量子コンピューターで使われるスイッチは、この「0であると同時に1でもある」という重ね合わせを利用して情報を表す。このため、「0か1か」の2種類しかない古典的コンピューターのスイッチに比べ、処理できる情報量が格段に大きくなるのだ。この情報単位を、古典的コンピューターが扱う二進法の「ビット」に対し、量子コンピューターでは「量子ビット」と呼ぶ。

もつれ＝一方を「観察」すると、他方の状態が「確定」

　「もつれ」とは、重ね合わせの状態にある2個以上の量子が相関し合い、一方を「観察」すると、その瞬間に他方の状態が「確定」する状態のことだ。

　例えば、量子AとBが「0であると同時に1でもある」という重ね合わせの状態にあり、同時にもつれているとする。このとき、観察によってAが「0」と分かった瞬間、Bは「1」に確定するといった現象が起こる。逆に、Aが「1」なら、Bは「0」に確定する。

　量子コンピューターは、複数の量子をもつれさせて計算を実行する。例えば、100個のもつれた量子のうち1つを「確定」した瞬間、他の99個の状態もすべて連鎖的に「確定」する。この性質を利用すると、電流を利用して段階的に情報を処理していく古典的コンピューターに比べ、量子コンピューターは超高速で計算できるようになる。

　量子コンピューターの基本性能は、「何個の量子をもつれた状態にできるか」によって決まる。この量子がもつれた数を、例えば「2量子ビット」「3量子ビット」などと表現する。一般的に、量子ビットが1増えると、1度に処理できる計算能力は2倍に向上する。なお、もつれは量子力学を応用する「暗号通信」の基盤技術としても使われている。

量子ともつれ
（出所）リコー経済社会研究所

　以上のように量子コンピューターの理屈は、なかなか直感的にすんなり理解するのは難しい。しかしその理屈はともかく、古典的なコンピューターと比べてある種の計算能力が桁外れに向上する量子コンピューターが実用化すると、わたしたちの仕事も大きく変わることになるはずだ。